Randomization Dependency: Incremental Examples

IRO aims to provide flexible while accurate description of randomization and relationship among randomized values using fundamental building blocks: mutable attributes and harmonizers. These elements can be wired up with macros to form a DAG-like dependency tree, such that a randomized element can depend on another randomization.

Note

The images in the following examples are generated using the embedded interface. In the viewport, you can focus on a selected prim by pressing “F”; and then you can press “Alt + Left Mouse Button” to rotate the active camera around the selected prim.

A Basic Example

Let’s start with a basic example: “Randomly scatter ten randomly colored cubes on a plane”. The corresponding description file is:

isaacsim.replicator.object:
  version: 0.4.x
  num_frames: 3
  seed: 0
  output_path: PATH_TO_OUTPUT
  simulation_time: 1
  gravity: 981

  dome_light:
    intensity: 3000
    subtype: dome
    type: light

  cube_size: 0.5
  basic_shape:
    count: 10
    type: geometry
    subtype: cube
    tracked: true
    physics: rigidbody
    color:
      distribution_type: range
      start:
        - 0.0
        - 0.0
        - 0.0
      end:
        - 1.0
        - 1.0
        - 1.0
    transform_operators:
      - translate:
          distribution_type: range
          start:
            - -300
            - $[/cube_size] / 2 * 100
            - -300
          end:
            - 300
            - $[/cube_size] / 2 * 100
            - 300
      - rotateY:
          distribution_type: range
          start: -180
          end: 180
      - scale:
        - $[/cube_size]
        - $[/cube_size]
        - $[/cube_size]

  plane:
    type: geometry
    subtype: plane
    tracked: true
    physics: collision
    color:
      - 0.5
      - 0.7
      - 0.7
    transform_operators:
      - scale:
        - 10
        - 10
        - 10

  screen_height: 2160
  screen_width: 3840
  focal_length: 14.228393962367306
  horizontal_aperture: 20.955
  camera_parameters:
    screen_width: $[/screen_width]
    screen_height: $[/screen_height]
    focal_length: $[/focal_length]
    horizontal_aperture: $[/horizontal_aperture]
    near_clip: 0.001
    far_clip: 100000
  default_camera:
    camera_parameters: $[/camera_parameters]
    transform_operators:
      - rotateY: 30
      - rotateX: -30
      - translate:
        - 0
        - 0
        - 500
    type: camera

By using the embedded interface, we can create such a scene:

Randomization Dependency

To take a step further, it’s tempting to “Randomly scatter 10 randomly colored cubes on a plane, with varying sizes from 0.5 to 1.5, and varying color from red to blue, the bigger the size, the redder it is while the smaller the size, the bluer it is”, we can do this by:

isaacsim.replicator.object:
  version: 0.4.x
  num_frames: 3
  seed: 0
  output_path: PATH_TO_OUTPUT
  simulation_time: 1
  gravity: 981

  dome_light:
    intensity: 3000
    subtype: dome
    type: light

  size_coef:
    count: 10
    distribution_type: range
    start: 0.0
    end: 1.0
  size_min: 0.5
  size_max: 1.5
  basic_shape:
    count: 10
    type: geometry
    subtype: cube
    tracked: true
    physics: rigidbody
    color:
    - 0.0 + $[/size_coef_$[index]] * 1.0
    - 0.0 + $[/size_coef_$[index]] * 0.0
    - 1.0 + $[/size_coef_$[index]] * -1.0
    size: $[/size_min] + $[/size_coef_$[index]] * ($[/size_max] - $[/size_min])
    transform_operators:
    - translate:
        distribution_type: range
        start:
        - -300
        - $[../size] / 2 * 100
        - -300
        end:
        - 300
        - $[../size] / 2 * 100
        - 300
    - rotateY:
        distribution_type: range
        start: -180
        end: 180
    - scale:
      - $[../size]
      - $[../size]
      - $[../size]

  plane:
    type: geometry
    subtype: plane
    tracked: true
    physics: collision
    color:
      - 0.5
      - 0.7
      - 0.7
    transform_operators:
    - scale:
      - 10
      - 10
      - 10

  screen_height: 2160
  screen_width: 3840
  focal_length: 14.228393962367306
  horizontal_aperture: 20.955
  camera_parameters:
    screen_width: $[/screen_width]
    screen_height: $[/screen_height]
    focal_length: $[/focal_length]
    horizontal_aperture: $[/horizontal_aperture]
    near_clip: 0.001
    far_clip: 100000
  default_camera:
    camera_parameters: $[/camera_parameters]
    transform_operators:
    - rotateY: 30
    - rotateX: -30
    - translate:
      - 0
      - 0
      - 1000
    type: camera

And we get:

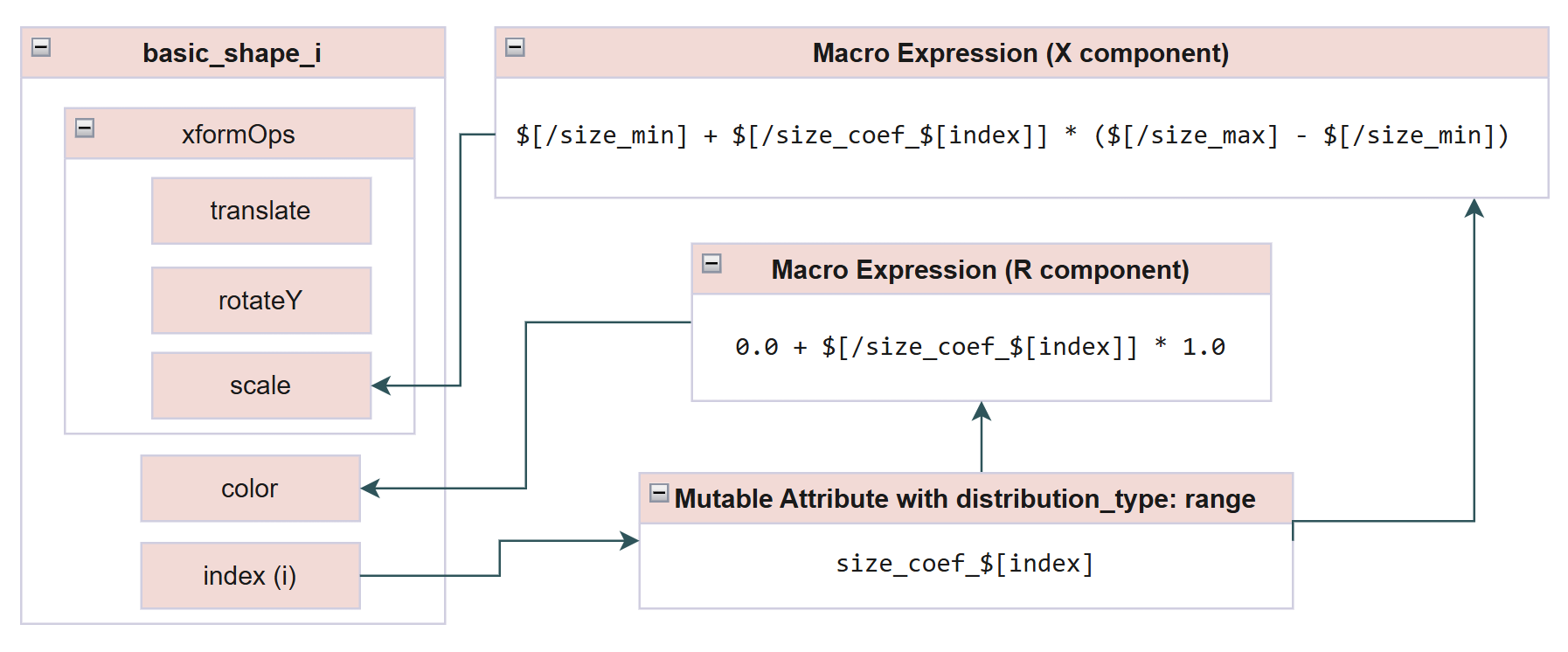
The bigger the redder, the smaller the bluer. This is achieved by dependent mutable attributes. The color is determined by linear interpolation between red and blue:

color:
- 0.0 + $[/size_coef_$[index]] * 1.0
- 0.0 + $[/size_coef_$[index]] * 0.0
- 1.0 + $[/size_coef_$[index]] * -1.0

Here

basic_shape:
  count: 10

resolves to

basic_shape_0:
  index: 0
basic_shape_1:
  index: 1
basic_shape_2:
  index: 2
...

And that goes similarly for

size_coef:
  count: 10
  distribution_type: range
    start: 0.0
    end: 1.0

And then for basic_shape_0, for example, the R channel of color, 0.0 + $[/size_coef_$[index]] * 1.0, will resolve to 0.0 + $[/size_coef_0] * 1.0 and $/size_coef_0 will be replaced with a randomized value between 0 and 1. Here is a DAG chart that shows the symbol resolution process:

Harmonization

Let’s try to “pack the above cubes into a big box and randomly place and rotate this big box around the up axis”.

The corresponding description file:

isaacsim.replicator.object:
  version: 0.4.x
  num_frames: 3
  seed: 0
  output_path: PATH_TO_OUTPUT
  simulation_time: 1
  gravity: 981

  dome_light:
    intensity: 3000
    subtype: dome
    type: light

  bin_pack_H:
    harmonizer_type: bin_pack
    bin_size:
    - 400
    - 300
    - 400
  size_coef:
    count: 50
    distribution_type: range
    start: 0.0
    end: 1.0
  size_min: 0.5
  size_max: 1.5
  bin_translate:
    distribution_type: range
    start:
    - -100
    - 150
    - -100
    end:
    - 100
    - 150
    - 100
  bin_rotate_Y:
    distribution_type: range
    start: -180
    end: 180
  basic_shape:
    count: 50
    type: geometry
    subtype: cube
    tracked: true
    physics: rigidbody
    color:
    - 0.0 + $[/size_coef_$[index]] * 1.0
    - 0.0 + $[/size_coef_$[index]] * 0.0
    - 1.0 + $[/size_coef_$[index]] * -1.0
    size: $[/size_min] + $[/size_coef_$[index]] * ($[/size_max] - $[/size_min])
    transform_operators:
    - translate: $[/bin_translate]
    - rotateY: $[/bin_rotate_Y]
    - transform:
        distribution_type: harmonized
        harmonizer_name: bin_pack_H
        pitch:
        - - -$[../../size] / 2 * 100
          - -$[../../size] / 2 * 100
          - -$[../../size] / 2 * 100
        - - $[../../size] / 2 * 100
          - $[../../size] / 2 * 100
          - $[../../size] / 2 * 100
    - scale:
      - $[../size]
      - $[../size]
      - $[../size]

  plane:
    type: geometry
    subtype: plane
    tracked: true
    physics: collision
    color:
      - 0.5
      - 0.7
      - 0.7
    transform_operators:
    - scale:
      - 10
      - 10
      - 10

  screen_height: 2160
  screen_width: 3840
  focal_length: 14.228393962367306
  horizontal_aperture: 20.955
  camera_parameters:
    screen_width: $[/screen_width]
    screen_height: $[/screen_height]
    focal_length: $[/focal_length]
    horizontal_aperture: $[/horizontal_aperture]
    near_clip: 0.001
    far_clip: 100000
  default_camera:
    camera_parameters: $[/camera_parameters]
    transform_operators:
    - rotateY: 30
    - rotateX: -30
    - translate:
      - 0
      - 0
      - 1500
    type: camera

Here, translate and rotateY defines the global movement of the big box (the bin), and transform is a harmonized mutable attribute. The global translate and rotateY has the same value for all basic shapes, though randomized per frame. This is why the mutable attributes are defined outside of the basic shapes and then referenced through macros. Had it been defined inside the xformOps list, each basic shape would have a different randomized value.

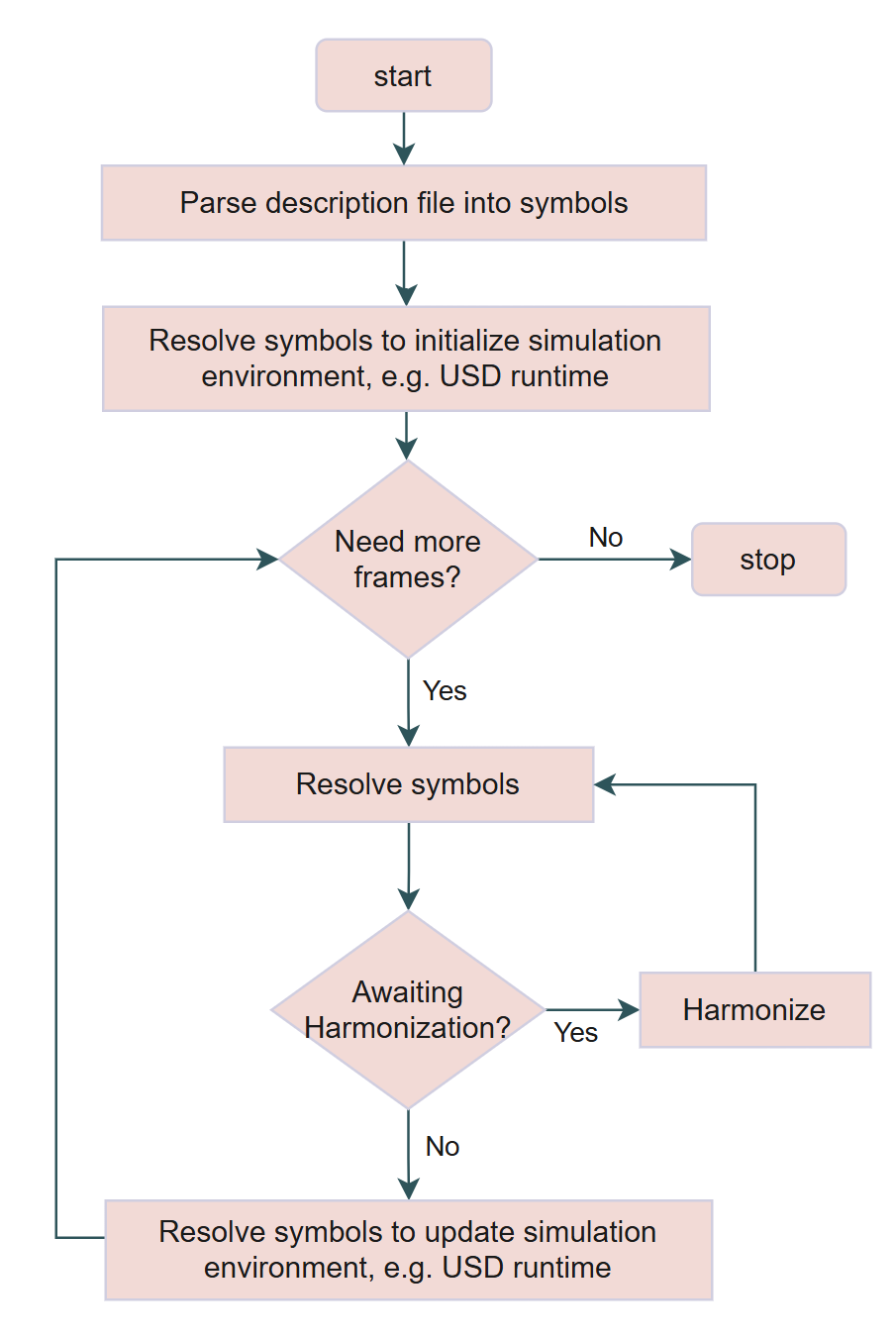
An Insight into the Simulation Workflow

During initialization, mutable attributes and harmonizers are initialized, and a dependency tree with mutable elements (such as mutable attributes with different distribution types, expressions with macros, and more) is created based on the description file, and then the USD runtime scene is initialized, loading all the prims that are about to be randomized.

Each frame, all the mutable attributes resolve for their values. Mutable attributes with macros, like channels of color and size in our examples resolve their dependent mutable elements (like macro expressions) recursively. The symbol resolution procedures are totally in description level, so it’s as if we are doing randomization on text; in this stage, the USD environment is not involved.

The Harmonization Process

A harmonized mutable attribute is a special mutable attribute that can’t be resolved by running resolution once, because it needs information from other mutable attributes sharing the same harmonizer. The first time we resolve the symbols, the attribute gets into an AWAITING_HARMONIZATION state, and then the harmonizer absorbs its pitch (in this case, the size of the cube):

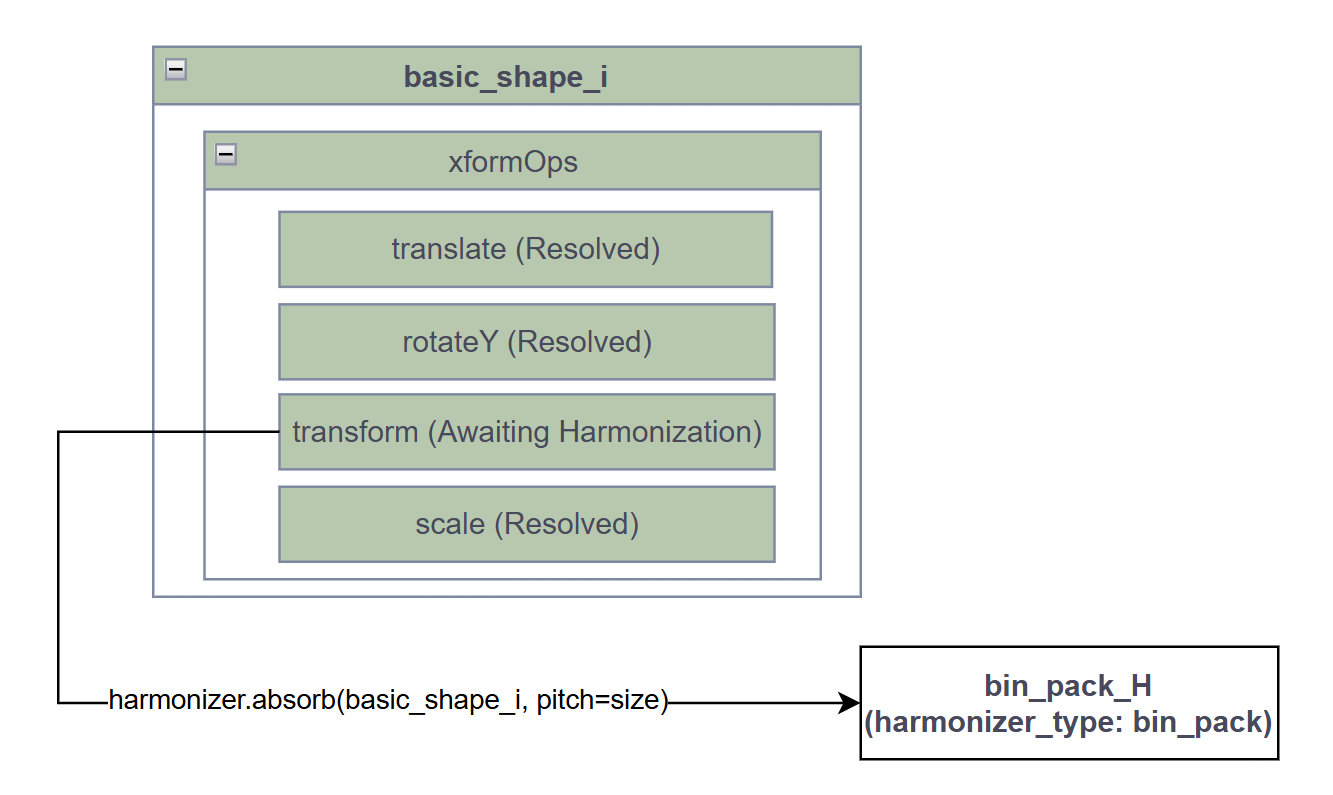
All non-harmonized attributes are resolved, which is necessary because harmonized attributes may depend on them. For example, an object can be randomized to use a different USD model with a different size bounding box, which can be the pitch to be absorbed by the harmonizer. The USD runtime is then updated based on non-harmonized attributes.

After getting all the information from the harmonized attributes, the harmonizer harmonizes. It now knows where each cube’s local transformations in the big box.

The system is in AWAITING_HARMONIZATION state if there is at least one attribute in this state, which means we need to resolve the whole description again. Now the corresponding values are propagated back to respective harmonized attributes.

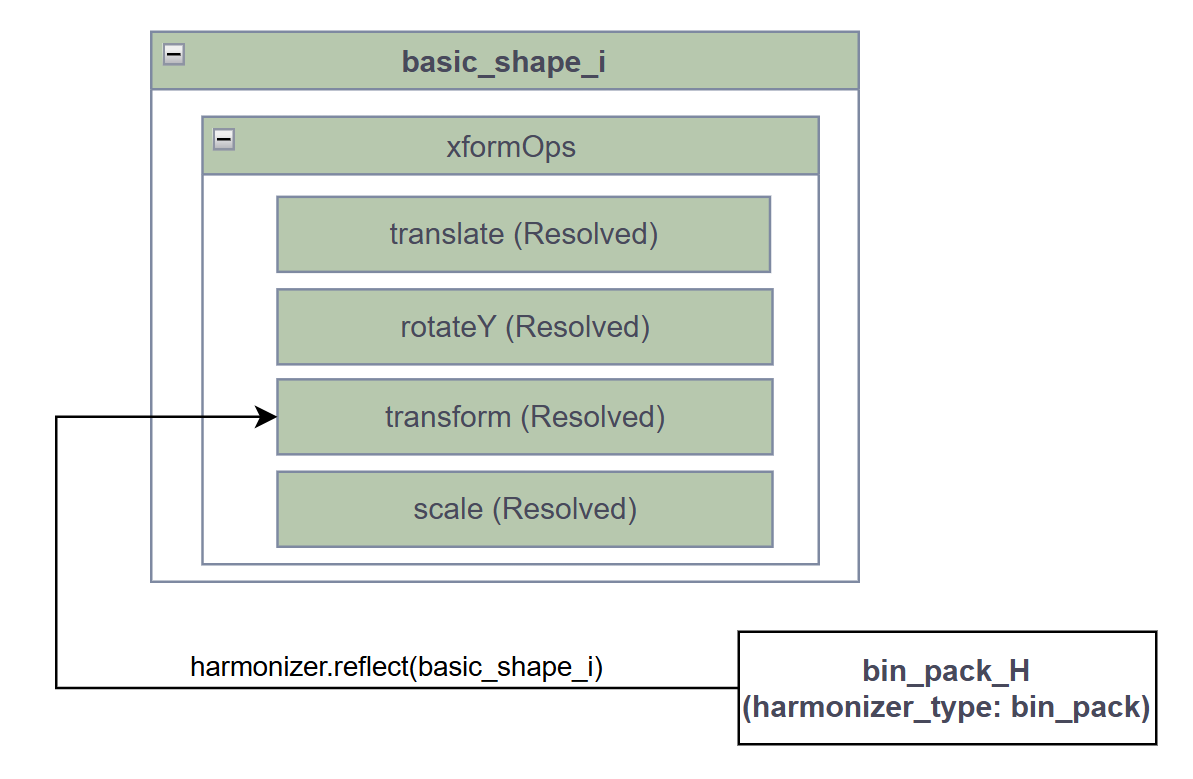
Now we have all the fixed numbers, we can use them to update the scene again. So, the whole workflow looks like: